TB_1_JNT
TB_1_JNT ---- giunto interno della capriata ----
Il TB_1_JNT è definito come il giunto di collegamento tra le aste di parete della reticolare (Wall Member - WM) e il corrente superiore o inferiore (Chord Memeber - CM).
Ricordiamo che:
- Wall Member - elemento di parete: è l'elemento della capriata che collega i due correnti (alle due estremità è caratterizzato, in genere, da un nodo TB_1_JNT); è, inoltre, sollecitato da una forza assiale costante.
- Chord Member - corrente: è l'elemento continuo della capriata TB_1; esso è caratterizzato da una sollecitazione assiale non costante, incrementata o ridotta attraverso le forze di scorrimento trasmesse dagli elementi di parete in corrispondenza di ogni nodo TB_1_JNT.
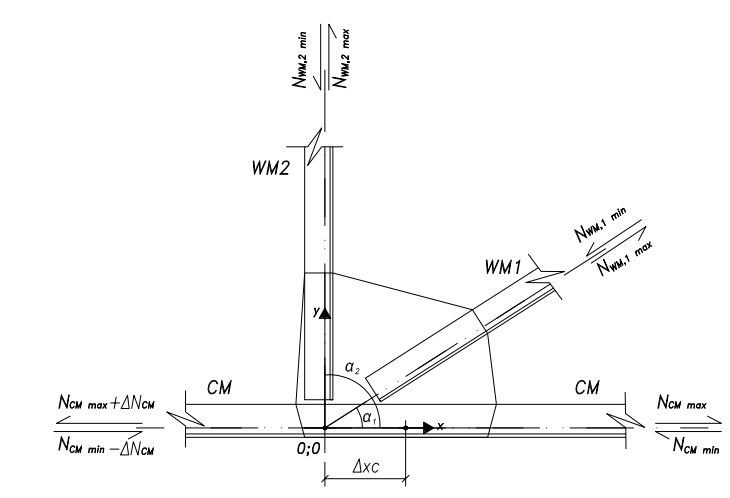
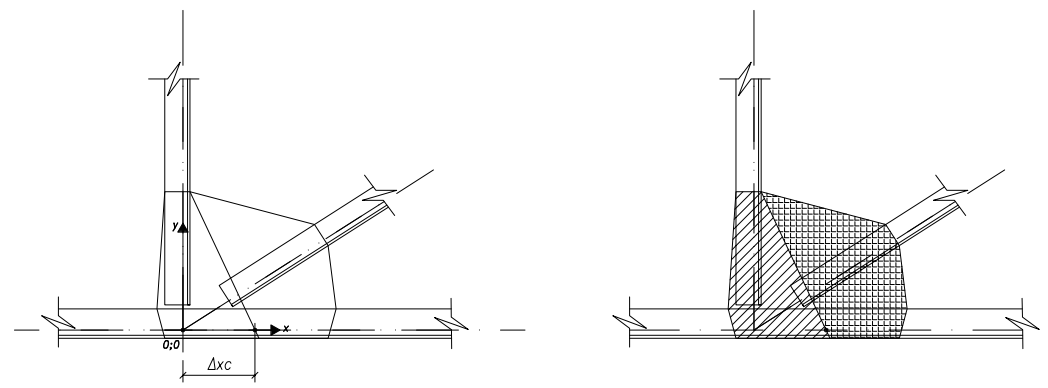
Un tipico giunto siffatto è rappresentato in figura sottostante, in cui:
- punto (0;0): origine del sistema di riferimento locale del giunto (x;y), individuato dall'intersezione delle linee baricentriche delle aste che convergono nel nodo;
- CM: (Chord Member) corrente inferiore o superiore della capriata;
- WM1, WM2: (Wall Member) aste di parete della capriata concorrenti nel giunto; in generale nel nodo generico avremo WMi, con "i" numero delle aste di parete convergenti nel nodo;
- α1, α2 :angolo tra asse del corrente e asse rispettivamente asta 1 e asta 2 (in generale avremo αi);
- Δxc: ascissa del baricentro dei connettori (bullonatura o saldatura) tra corrente e piastra: è l'ascissa che definisce il centro della connessione Chord-Plate.
Ogni asta è in generale soggetta ad un'azione assiale positiva (se di trazione) o negativa (se di compressione).
La verifica del nodo non viene eseguita per ogni combinazione di carico, ma il calcolo viene svolto su dei "casi limite", considerando (a favore di sicurezza) le massime sollecitazioni (in valore assoluto) su ogni asta.
La massima sollecitazione su ciascuna membratura viene determinata da CalcS tramite l'inviluppo delle combinazioni di carico, se il modello importato possiede queste informazioni; altrimenti CalcS stima questa sollecitazione con il massimo o il minimo valore dello sforzo assiale che può supportare l'asta, calcolati secondo le luci di libera inflessione così come definiti nelle Ipotesi sulle lunghezze di libera inflessione della capriata reticolare TB_1 (in questo secondo caso il giunto è calcolato "a ripristino"). L'azione assiale nelle aste è considerata applicata lungo l'asse baricentrico di ogni profilo.
ΔNCM è la forza di scorrimento nel giunto; in generale è calcolata da CalcS nel seguente modo:
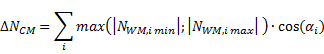
Nel macroelemento TB_1, CalcS calcola la forza di scorrimento in ogni giunto TB1_JNT come da formula precedente; nella singola scheda di calcolo, invece, questo valore viene "ereditato" dal valore di sollecitazione imposto nella scheda di calcolo del profilo scelto come Chord (si consiglia di usare la formula proposta).
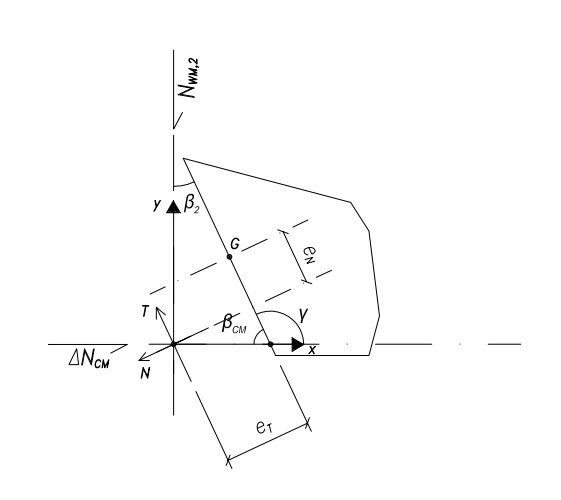
A partire dal punto (Δxc; 0) si possono tracciare, per ciascuna asta di parete, due rette, che dividono la piastra in due parti; tra le infinite rette che si possono tracciare con punto base (Δxc; 0), si considerano, per ogni asta, quelle che intercettano il profilo dell'asta stessa, con inclinazione massima e minima rispetto al corrente.
Per esempio, nella figura sottostante si individuano le due rette per l'asta di parete WM1 (rette con giacitura "a" e "c").
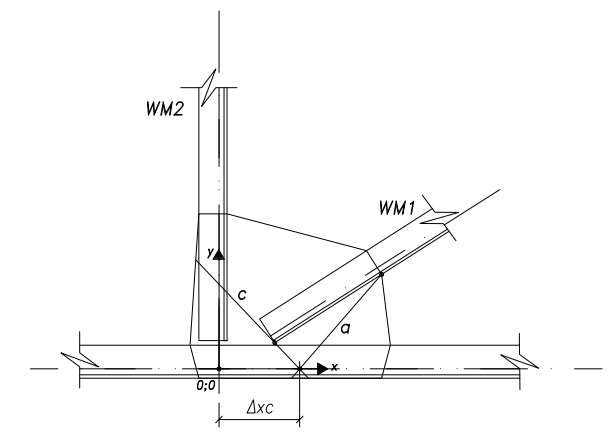
Nella figura sottostante le rette per l'asta di parete WM2 (rette con giacitura "b" e "d").
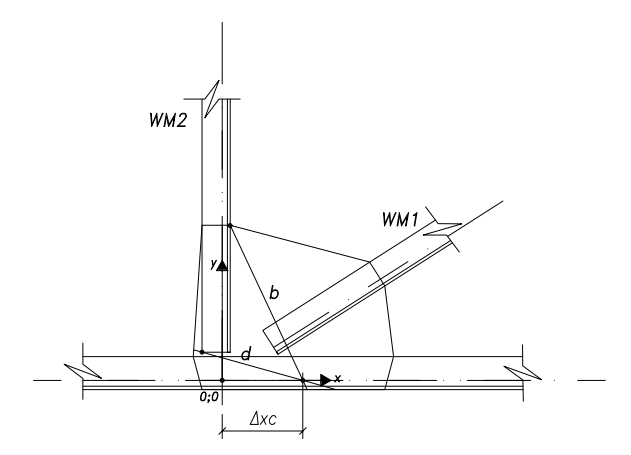
Individuate tutte le possibili rette costruite nel modo sopra descritto, considerando ciascuna di esse, di volta in volta, si esegue l'equilibrio di ognuna delle parti di piastra "tagliata" e si effettuano le verifiche di resistenza.
Ad esempio, considerando la figura precedende, prendiamo in esame la retta "b": essa divide la piastra del nodo in due parti, come da figure sottostanti:
Consideriamo la parte di destra della piastra; in essa si stimano per eccesso (a favore di sicurezza) le risultanti N,T,M nel modo seguente:
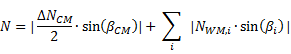NB: sommatoria eseguita solo per le aste Wm,i interamente a sinistra della linea di taglio!
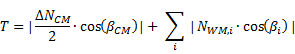
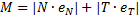
in cui:
ΔNCM = forza di scorrimento nel giunto.
βCM = angolo formato dall'asse del Chord con la retta che taglia la piastra;
β2 = angolo formato dall'asse dell'asta di parete WM2 con la retta che taglia la piastra (in generale βi angolo formato dall'asse dell'asta di parete i-esima e la retta che taglia la piastra);
eT = distanza tra il baricentro geometrico della sezione della piastra in corrispondenza del taglio e il punto (0;0), in direzione perpendicolare alla linea di taglio;
eN = distanza tra il baricentro geometrico della sezione della piastra in corrispondenza del taglio e il punto (0;0), in direzione parallela alla linea di taglio.
La verifica di resistenza della piastra è soddisfatta se risulta verificata la relazione:
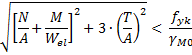
dove:
- A è l'area della sezione della piastra in corrispondenza del "taglio" considerato;
- Wel è il modulo di resistenza elastico (la sezione della piastra, per qualsiasi linea di taglio, è rettangolare).
Come anticipato precedentemente, questa verifica viene effettuata per tutte le possibili linee di taglio della piastra, così come descritte sopra.
Acquista:
| Resta informato:
| Formazione su CalcS:
